Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka'> 3.3.1 Occupation spectrale
Up One Level Les Modulations à Phase Continue pour la Conception d'une Forme d'Onde Adaptative
Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka		 Contents
Previous: Up: 3.3 Performances des Modulations Next:

3.3.1 Occupation spectrale

Ce paragraphe concerne l'étude des propriétés spectrales des signaux CPM. Cette étude se justifie par l'importance d'une exploitation optimale de ressources spectrales de plus en plus réduites. La capacité totale d'un système de transmissions de données multimédia est directement liée à l'efficacité spectrale de la forme d'onde adoptée. Afin de limiter les niveaux des interférences, les contraintes concernant la puissance transmise en dehors de la bande spectrale allouée sont primordiales. Ainsi, nous devons tenir compte de la puissance transmise hors bande pour une sélection plus efficace de la CPM.


Bien qu'elle soit une propriété assez intéressante, l'enveloppe constante du signal est souvent pénalisante d'un point de vue spectral. Elle induit une bande occupée bien plus élevée que dans le cas des signaux avec fluctuation d'enveloppe. Dans le cas des modulations CPM, ce handicap peut être compensé grâce à la forte corrélation des signaux CPM à réponse partielle. L'adoption d'une longueur de la réponse en fréquence $ L>1$ introduit une corrélation dans le signal, elle permet ainsi de réduire l'occupation spectrale des signaux CPM. Cette réduction est d'autant plus importante que le paramètre $ L$ est élevé. Le spectre des signaux CPM est aussi fortement dépendant de la réponse en fréquence adoptée, de l'ordre de la modulation ainsi que de l'indice de modulation. Les performances spectrales des signaux CPM doivent êtres optimisées en assurant les performances en puissances requises.


Des techniques d'estimation des spectres des signaux CPM ont été proposées dans [5,10], ces méthodes semi-analytiques sont basées sur des calculs de l'autocorrélation de ces signaux permettant d'en déduire une estimation du spectre [9]. L'intérêt de ces techniques est qu'elles nécessitent peu de ressources de calcul numérique par rapport aux autres méthodes classiques. Aujourd'hui, que nous disposons de calculateurs plus performants, on a opté pour la méthode du périodogramme pour estimer les spectres des signaux CPM. Dans ce calcul, on considère la moyenne des transformées de Fourier calculées sur plusieurs fenêtres d'observation du signal.
Soit $ x$ le signal échantillonné de taille $ N_s$ et dont nous voulons estimer la densité spectrale de puissance:

$\displaystyle x=\left(x_1,\,x_2,\cdots \, x_{N_s-1},\,x_{N_s}\right)$ (3.4)

Soit $ m$ un entier de la forme $ m=N_s/l$, où $ l$ est un entier diviseur de $ N_s$, on définit alors la fenêtre $ w$ par:
$\displaystyle w(i)=$   \begin{displaymath}\begin{cases}1& 0\leq i\leq m-1\\ 0& \textrm{sinon} \end{cases}\end{displaymath}  

Souvent $ m$ est de la forme d'une puissance de $ 2$ ce qui va permettre d'effectuer des algorithmes rapides pour effectuer la transformée de Fourier. Une version décalée de $ d$ termes de $ w$ notée $ w_d$ est définie par $ w_d(i)=w(i-md)$. Notons $ S_x(f)$ la densité spectrale de puissance du signal $ x$, on peut alors l'estimer par:

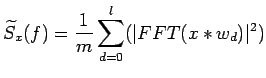$\displaystyle \widetilde{S}_x(f)=\frac{1}{m}\sum_{d=0}^{l}(\vert FFT(x*w_d)\vert^2)$    

La fenêtre $ w$ peut prendre une autre allure qu'une fenêtre rectangulaire, parmi ces fenêtres on trouve celles de Hamming, de Hanning et de Blackman. Lors des simulations présentées dans le paragraphe suivant, une fenêtre de Hanning a été utilisée.

Sous-sections

Up One Level Les Modulations à Phase Continue pour la Conception d'une Forme d'Onde Adaptative
Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka		 Contents
Previous: Up: 3.3 Performances des Modulations Next:
Documentation released on .
Back to the Homepage.