3.2.2 Représentation Treillis des CPM

Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka'> 3.2.2 Représentation Treillis des CPM

3.2.2 Représentation Treillis des CPM

Soit

un entier positif inférieur à

. A un instant

tel que $nT \leq t \leq (n+1)T$ la phase du signal en bande de base peut être décomposée sous la forme suivante ^3.1:

$\displaystyle \varphi(\underline{a},t)$	$\displaystyle =$	$\displaystyle 2\pi h \,a_{n}\,q(t-nT)+2\pi h \sum_{\scriptstyle k=n-L+1}^{\scriptstyle n-1}a_{k}q(t-kT)+\pi h\sum_{\scriptstyle k=0}^{\scriptstyle N-L}a_{k}$	(3.3)
	$\displaystyle =$	$\displaystyle 2\pi h \,a_{n}\,q(t-nT)+\phi_{n}(t)+\theta_{n}$

Avec:

$\displaystyle \phi_n(t)$	$\displaystyle =$	$\displaystyle 2\pi h\sum\limits_{k=n-L+1}^{n-1}a_{k}\,q(t-kT)$
$\displaystyle \theta_{n}$	$\displaystyle =$	$\displaystyle \pi h \sum\limits_{k=0}^{n-L} a_{k}$

En considérant une valeur de la phase modulo $2\pi$ , la valeur de $\theta_n$ ne peut prendre que

valeurs, suivant la parité du numérateur de l'indice de modulation, à savoir

. Plus précisément:
Si

est pair, $\theta_n$ varie dans l'ensemble

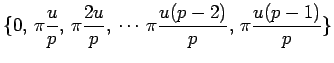
$\displaystyle \{0,\, \pi\frac{u}{p},\, \pi\frac{2u}{p},\, \cdots \, \pi\frac{u(p-2)}{p},\, \pi\frac{u(p-1)}{p}\}$

est impair, $\theta_n$ varie dans l'ensemble

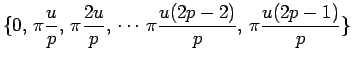
$\displaystyle \{0,\, \pi\frac{u}{p},\, \pi\frac{2u}{p},\, \cdots \, \pi\frac{u(2p-2)}{p},\, \pi\frac{u(2p-1)}{p}\}$

La valeur de $\theta_n$ définit l'état de la phase du modulateur. Le terme $\phi_n(t)$ représente la contribution des symboles transmis entre les instants et . Ce terme est entièrement défini par le vecteur $(a_{n-L+1},a_{n-L+2},\cdots,a_{n-1})$ . Quand au premier terme de l'équation 3.3 il représente la contribution du $n^{\textrm{i\\lq eme}}$ symbole.

En conclusion, le signal transmis pendant l'intervalle de temps $[nT\,(n+1)T]$ dépend du dernier symbole émis $a_{n}$ mais aussi de l'état du modulateur à l'instant défini par:

$\displaystyle \sigma_{n}=(\theta_{n},a_{n-L+1},a_{n-L+2},\cdots,a_{n-1})$

L'émission de ce symbole fait passer le modulateur dans un autre état à l'instant

qui est donné par:

$\displaystyle \sigma_{n+1}=(\theta_{n+1},a_{n-L+2},a_{n-L+3},\cdots,a_n)$

La valeur de $\theta_{n+1}$ s'obtient à partir de celle de $\theta_n$ comme suit:

$\displaystyle \theta_{n+1}=\left(\theta_{n}+\pi h a_{n-L+1}\right) \mod[2\pi]$

La description précédente permet d'associer une structure treillis à une modulation CPM, les états de ce treillis sont les $\sigma_{n}$ définis plus haut, et les transitions sont données par le couple ( $\sigma_{n}$ ,

). Le treillis comporte ainsi $pM^{L-1}$ ou $2pM^{L-1}$ états et $pM^{L}$ ou

transitions.

Exemple
Considérons une CPM binaire avec une réponse en fréquence rectangulaire de longueur notée 1REC, l'indice de modulation est ^3.2. Dans ce cas, l'état de la phase peut prendre 4 valeurs possibles modulo $2\pi$ , ces états sont $\{\pi/2,\, \pi,\, 3\pi/2,\, 2\pi\}$ (Les états zéros et $2\pi$ sont identiques). Dans cet exemple d'une CPM à réponse totale, l'état du modulateur se réduit à l'état de sa phase. sachant que le symbole d'entrée peut prendre seulement deux valeurs possibles, nous pouvons conclure qu'il existe 8 transitions dans le treillis. Par conséquent, sur la durée d'un symbole, il existe 8 formes possibles du signal en sortie du modulateur CPM. Les différentes trajectoires de la phase $\varphi(t)$ sont illustrées sur la figure 3.3.

**Figure 3.3:** Différentes trajectoires de phase dans le cas de la CPM 1REC binaire avec un indice
$\includegraphics[width=6.5cm]{msk_treillis_original.eps}$

**Figure 3.4:** Différentes trajectoires de phase (Modulo $2\pi$ ) dans le cas d'une 1REC binaire avec un indice
$\includegraphics[width=6.5cm]{msk_treillis_mod2pi.eps}$

Pour une meilleure visualisation du treillis, les différentes trajectoires de la phase sont considérées modulo $2\pi$ . La figure 3.4 illustre la forme du treillis de la CPM considérée. Comme on peut le remarquer, les états et les transitions dans le treillis varient avec le temps, suivant que l'on se situe à des multiples pairs ou impairs de la durée d'un symbole. Cela va ajouter une complexité supplémentaire dans le processus de décodage.

Dans [46], Rimoldi a proposé une décomposition du signal CPM qui permet d'avoir un treillis invariant dans le temps dont le nombre d'états ainsi que le nombre des transitions sont indépendants de la parité de . Cette décomposition est décrite dans l'annexe B et elle sera adoptée dans la suite du manuscrit.

Notes

... suivante ^3.1: pour
...\space ^3.2: Cette modulation est connue sous le nom de MSK

Back to the Homepage.