Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka'> 2.2 Etude de la Capacité du Canal
Up One Level Les Modulations à Phase Continue pour la Conception d'une Forme d'Onde Adaptative
Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka		 Contents
Previous: Up: 2. Canal Satellite en Next:

2.2 Etude de la Capacité du Canal

Avant toute conception d'une chaîne de transmission, et notamment la sélection de la forme d'onde, la nature ainsi que les propriétés du canal utilisé doivent êtres étudiés. Puissance du bruit, type et stationnarité du canal, sont des paramètres dont la connaissance a priori est primordiale pour un choix efficace de la forme d'onde. Cette connaissance permet ensuite d'évaluer la capacité du canal sachant la forme d'onde adoptée. D'un point de vue opérateur, les informations relatives aux conditions de propagation sont essentielles pour une première évaluation de la capacité du système ainsi que la qualité et la nature du service qu'il pourra proposer. Bien qu'il nécessite une complexité supplémentaire, un système dynamique qui évolue en fonction des conditions de propagation est bien plus efficace qu'un système non adaptatif.


Dans ses travaux, Shannon [49] a évalué la capacité d'un canal de propagation gaussien en fonction du rapport signal sur bruit et de sa largeur de bande. La capacité (exprimée en bit/s) peut se définir par le débit d'information maximal que peut supporter le canal tout en assurant une transmission sans erreur. Toutefois, dans ses travaux, Shannon n'indique pas de moyen et notamment de processus de codage canal permettant d'atteindre cette capacité limite.
Dans le cas d'une transmission sur deux voies en quadrature sur un canal gaussien de largeur $ W\,Hz$, et pour un rapport signal sur bruit par symbole $ E_s/N_0$, où $ E_s$ est l'énergie par symbole émis et $ N_0/2$ la densité spectrale de puissance du bruit, la capacité maximale est donnée par:

$\displaystyle C=W\log_2\left(1+\frac{E_s}{N_0}\right) \left(bit/s\right)$ (2.1)

Ici, on suppose que la bande du signal est liée au rythme symbole $ T_s$ par le premier critère de Nyquist, soit $ W=\frac{1}{T_s}$ [54].


Considérons une forme d'onde donnée et notons par $ R$ le débit utile des bits d'information. Ce débit binaire est toujours inférieur à la capacité maximale du canal $ C$. L'efficacité spectrale de cette forme d'onde, notée $ \eta$, est donnée par le rapport du débit utile sur la largeur de bande du canal, soit:

$\displaystyle \eta=\frac{R}{W}$    

Cette quantité représente aussi le nombre de bits d'information que nous pouvons transmettre par $ Hz$ et par seconde. Elle vérifie les contraintes suivantes:
$\displaystyle 0<\eta<\frac{C}{W}$      
$\displaystyle E_s=\eta E_b$      

$ E_b$ est l'énergie d'un bit utile (bit d'information), la première condition découle de la définition même de la borne de Shannon, alors que la seconde traduit le fait que l'efficacité spectrale est égale au nombre de bits d'information transmis suite à la transmission d'un symbole dans le canal. En combinant ces deux équations avec la relation 2.1 on peut écrire l'inégalité 2.2. Cette inéquation relie l'énergie transmise par bit à l'efficacité spectrale de la forme d'onde, c'est une condition nécessaire et suffisante pour assurer une transmission numérique sans erreur.

$\displaystyle E_b/N_0>\frac{2^{\eta}-1}{\eta}=\left(E_b/N_0\right)_{min}(\eta)$ (2.2)

L'équation 2.2 illustre aussi l'existence d'un compromis entre l'efficacité spectrale et la puissance requise par bit d'information. A largeur de bande constante, une augmentation de $ \eta$ nécessite un niveau de puissance par bit d'informations plus élevé, où d'une manière équivalente puissance transmise plus élevée. La même équation montre aussi l'existence d'une valeur seuil du rapport $ E_b/N_0$ en dessous de laquelle il est théoriquement impossible d'assurer une communication sans erreurs, et ceci quelque soit la largeur du canal dont on dispose. Cette valeur est obtenue quand l'efficacité spectrale tend vers zéro:

$\displaystyle \left(E_b/N_0\right)_{lim}=\lim_{\eta \rightarrow 0}\frac{2^{\eta}-1}{\eta}=\ln(2)=-1.6 dB$ (2.3)


Le calcul effectué ci-dessus est indépendant du type de la forme d'onde adoptée par la chaîne de communication. Une évaluation de la capacité du canal en fonction des propriétés du canal ainsi que la constellation de symboles de la forme d'onde, constitue une approche bien plus précise pour le calcul de la capacité du canal. Dans le cas d'une modulation linéaire avec une constellation à M symboles complexes $ (a_0,a_1,\ldots,a_{M-1})$, émis d'une façon équiprobable, la formule de la capacité du canal devient [54]:

$\displaystyle \eta(M)=\log_2(M)-\frac{1}{M} \sum\limits_{i=0}^{M-1}E\left(\log... ...-1} \exp\left(-\frac{\vert a_i-a_j+n\vert^2-\vert n\vert^2}{N_0}\right)\right)$ (2.4)

Où $ n$ désigne un bruit additif blanc gaussien centré de variance $ N_0/2$, le symbole $ E$ désigne l'espérance mathématique. La figure 2.2 illustre l'évolution de cette capacité dans le cas de quelques formes d'onde M-aires en fonction du rapport $ E_b/N_0$.
Figure 2.2: Efficacité spectrale de quelques modulations M-aires linéaires en fonction du $ E_b/N_0$
\includegraphics[width=10cm]{channel_capacity_ebno.eps}
A faible rapport $ E_b/N_0$ la capacité maximale du canal est quasiment identique pour toutes les formes d'onde. Il est ainsi inutile d'adopter des modulations d'ordre élevé dans cette région même si le processus de codage canal permet d'approcher sa capacité maximale. Par contre, dans le cas d'un fort rapport $ E_b/N_0$, les formes d'ondes d'ordre élevé sont plus attractives d'un point de vue efficacité spectrale. On peut aussi remarquer que la capacité maximale d'une modulation M-aire ,qui est égale à $ \log_2(M)$, est théoriquement irréalisable notamment à faible rapport signal sur bruit. Ce fait traduit la nécessité de l'utilisation d'un processus de codage canal pour assurer une communication sans erreurs. Bien évidemment, le rendement du code optimal est fonction du rapport $ E_b/N_0$. Plus précisément, en notant $ \rho_M$ le taux de codage optimal qui permet d'atteindre la capacité maximale du canal $ \eta_M$ d'une modulation M-aire donnée, on peut exprimer ce taux de codage optimal par l'équation:

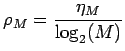$\displaystyle \rho_M=\frac{\eta_M}{\log_2(M)}$    

La figure 2.3 illustre l'évolution du rendement du code optimal en fonction du rapport $ E_b/N_0$.
Figure 2.3: Taux de codage optimal en fonction du $ E_b/N_0$ pour quelques modulations M-aires
\includegraphics[width=10cm]{opt_code_rate.eps}
A un même rapport $ E_b/N_0$, les modulations d'ordre moins élevé nécessitent un taux de codage plus élevé, ceci est dû au fait que ces formes d'ondes sont plus efficaces en puissance que les modulations à ordre plus élevé. Autre que le rendement, ce résultat ne fournit aucune information concernant le code qui permet d'atteindre la capacité maximale. Ce sujet est aujourd'hui au centre des activités de recherche dans le domaine de la théorie de l'information.


En conclusion, le choix de la modulation et du taux de codage doit s'effectuer d'une façon conjointe. Ce choix doit tenir compte des conditions de propagation. Dans le cas d'un canal de propagation à forte fluctuation du rapport $ E_b/N_0$, comme c'est le cas du canal satellite en bande Ka, une forme d'onde donnée ne peut pas être optimale en tout points de fonctionnement. Si notre sélection favorise l'efficacité en puissance, les ressources en spectre seront alors mal exploitées lors de bonnes conditions de propagation. Ce choix aboutira alors à une faible capacité du système et donc une mauvaise rentabilité économique. D'autre part, si l'efficacité en spectre est favorisée, et sachant que l'on se situe souvent à des faibles et moyens $ E_b/N_0$, le système aura une faible disponibilité et il devient donc difficile d'assurer la qualité de service requise.


Dans la pratique, il se trouve que la capacité d'une forme d'onde est affectée par d'autres éléments extérieurs telles que la dégradation due à une synchronisation imparfaite. Les non-linéarités du canal ainsi que celles des amplificateurs peuvent aussi dégrader les performances de la forme d'onde par rapport aux performances théoriques. L'ampleur de la dégradation varie d'une forme d'onde à une autre. En particulier, la sensibilité aux non-linéarités est fortement liée aux fluctuations de l'enveloppe du signal. Ainsi, les formes d'onde à faible fluctuation d'enveloppe montrent une meilleure résistance aux non-linéarités que celles à forte fluctuation d'enveloppe.

Up One Level Les Modulations à Phase Continue pour la Conception d'une Forme d'Onde Adaptative
Application aux Futurs Systèmes Multimédia par Satellite en Bande Ka		 Contents
Previous: Up: 2. Canal Satellite en Next:
Documentation released on .
Back to the Homepage.